Mathematical model for the transmission dynamics of Leptospirosis in human population

Abstract

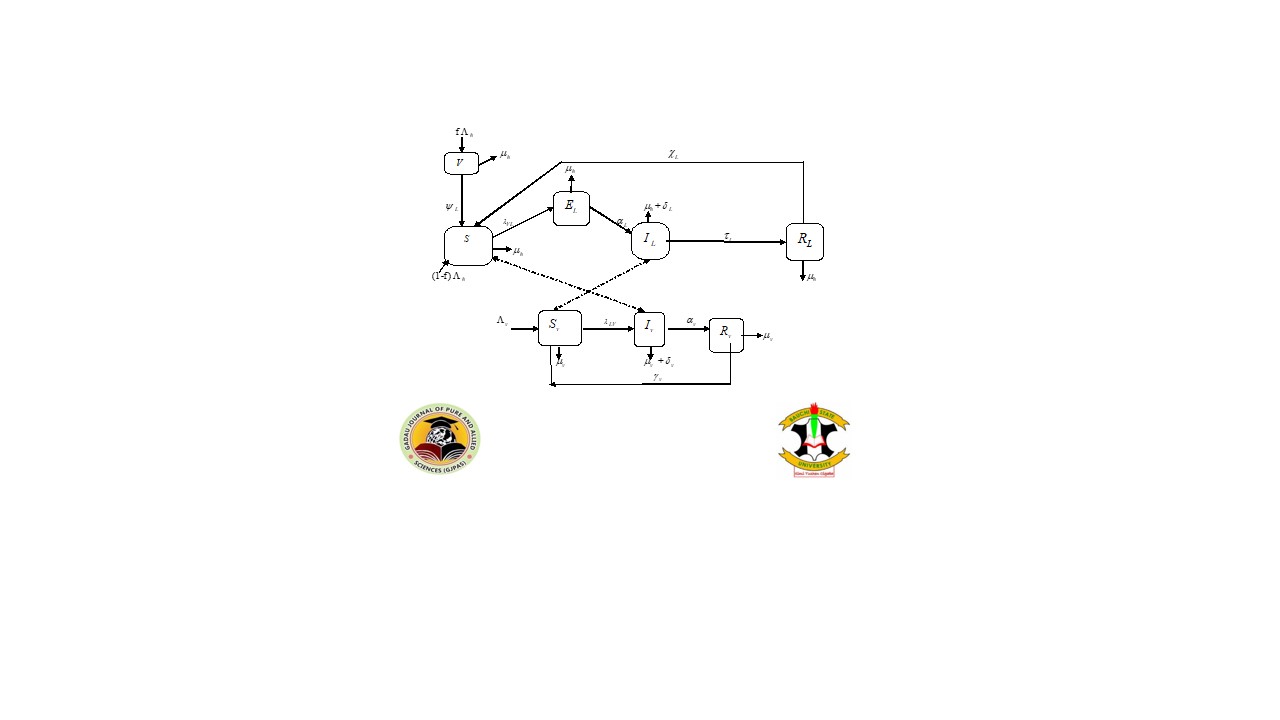
Leptospirosis infection is a contractable disease which is caused by bacteria known as Leptospira. It can lead to serious complications and can pose serious health challenge if not treated promptly and effectively. This paper considered the formulation of a model with eight compartments for leptospirosis transmission in human population to study and analyze the dynamics of the infection. The threshold parameter known as basic reproduction number, a vital quantity for estimating the trends of the spread of the disease was derived. It was discovered from the analysis that model (1) exhibits a disease-free equilibrium point. This was further verified as being both locally and globally asymptotically unchanging whenever the effective basic reproduction number is less than one. Model (1) has an endemic equilibrium point which was as well proved to be both locally and globally asymptotically unchanging whenever the effective basic reproduction number is greater than unity. The study extends its analysis to verify backward bifurcation phenomenon of leptospirosis infection and was ascertained to exist due to loss of temporary immunity as human continue to interact with domestic animals, rodents found in stores and the use of recreational centres such as swimming pool after treatment. Finally, the work suggested the incorporation of vaccination as a control measure to prevent re-infection to human from leptospirosis disease.