Predictive validity of SSCE grades and UTME points on final CGPA of students of Bauchi State University Gadau, Bauchi State
DOI:
https://doi.org/10.54117/gjpas.v1i1.6Keywords:
Correlation, Final CGPA, Regression, SSCE grades, UTME pointsAbstract
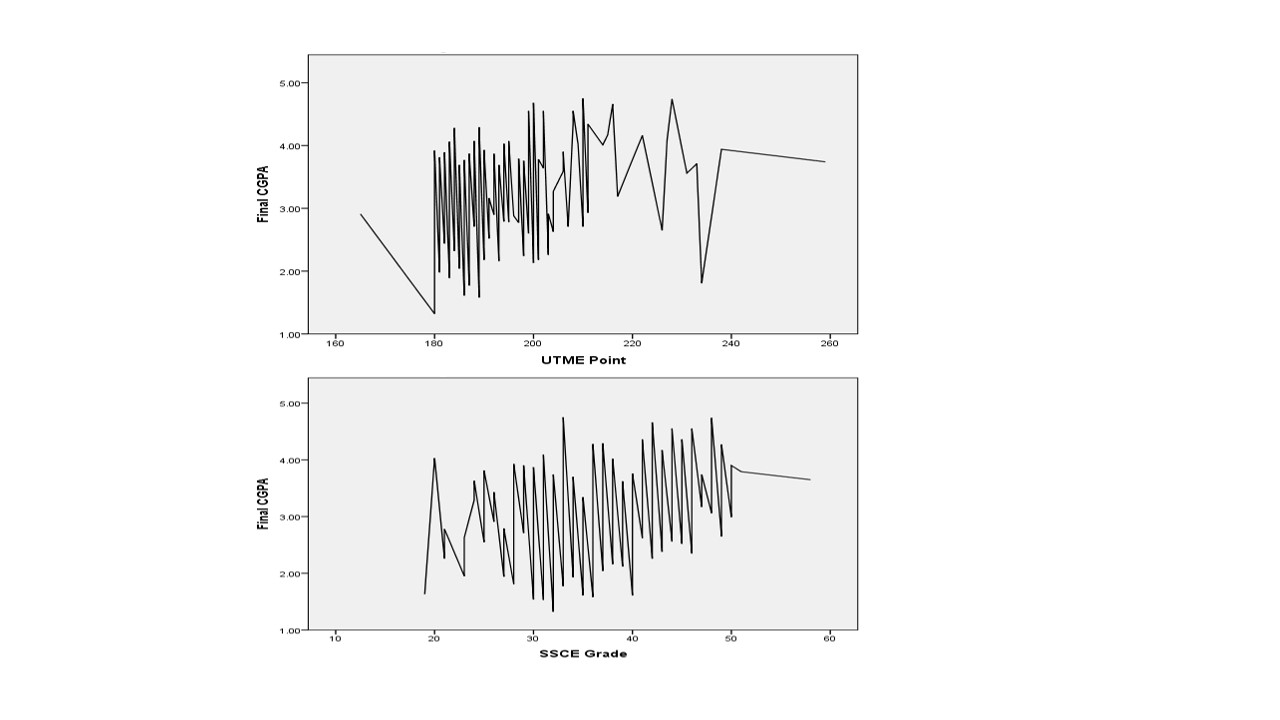
Cumulative Grade Point Average (CGPA) is a major indicator of students’ academic performance in Nigerian university system and the final class of degree to be awarded to a student solely relies on his final CGPA. The academic entry requirements into the universities are Senior Secondary Certificate Examination (SSCE) grades and Unified Tertiary Matriculation Examination (UTME) points. One may naturally therefore, expect paramount dependency of student’s final CGPA on his SSCE grades and UTME points on entry. This study used multiple linear regression based on ordinary least squares with SSCE grades and UTME points on entry as predictors of final CGPA of students. We also used Pearson correlation to ascertain relationships between each predictor variable and the dependent variable. Results for both methods revealed that final CGPA of students in the university is not strongly determined by their SSCE grades and UTME points.
References
Adeyemi, T.O. (2013). Entry Qualification as Predictors of Performance in the Final Year Bachelor of Education Degrees in Universities in Ondo and Ekiti States, Nigeria. American Journal of Economics 3(1): 43-51
Afu, M.O. (2017). Predictive Validity of UTME and Post-UTME scores on first Year Students’ Performance in Four Departments in University of Abuja. International Journal of Education and Evaluation 3(4)
Arnab, R. (2017). Survey Sampling Theory and Applications. Academic Press.
Babalola, I. B. (2015). Relationship between entry qualification and performance in A’ level chemistry: A case study of School of Basic and Remedial Studies Yobe State University, Damaturu, Yobe State. African Educational Research Journal 3(2): 2354-2160
Dauda, M. K., Magaji, A. S., Alfaki, H. A., Usman, M. A. and Tanko, I. S. (2020). Analysis of Entry Requirement and Cumulative Grade Point Average of Students to Predict their Final Year Graduating CGPA in Kaduna State University. Journal of the Nigerian Association of Mathematical Physics 58: 69-80.
Faleye, B.A. (2015). Predictive Validity of Students’ Entry Qualifications into Mathematics Programme in Nigeria’s Osun and Oyo States’ Colleges of Education. Journal of Education and Human Development. 4 (4): 209 - 217
Gujarati, (2004). Basic Econometrics Fourth Edition. The McGraw−Hill Companies
Jangson, K.I. and Igomu A.C. (2014). Entry Qualifications as Predictor of Students’ Final Year Academic Performance in Nasarawa State College of Education Akwanga Nigeria. American International Journal of Research in Humanities, Arts and Social Sciences. 2328-3734
Kolawale E. B., Oginni I. O. and Fayomi E. O. (2011). UTME and POST-UTME as predictors of students’ academic performance in chemistry in Nigerian universities. OIDA International Journal of Sustainable Development 2(9): 23-28
Ogbonnaya, N.P., Okpuruka, P.O.U., Iheanacho, P.N. and Ndu, A. (2014). Students’ Entry Qualification and Academic Performance in Basic Schools of Nursing in Enugu State between 1995 and 1999. Creative education 5: 719 - 727
Okafor, F. C. (2002). Sample Survey Theory with Applications. Afro-Orbis Publications Ltd Nsukka
Okobia, D.O. (2015) Predictive Efficacy of Utme, Ist and Utme Plus on Degree Students’ Cumulative Grade Points Average: A Case Study of College of Education, Agbor, Nigeria. International Journal of Innovative Research & Development 4(6)
Sa’adatu, A, and Francisca, N. O. (2019). Predicting Students’ First-Year Academic Performance Using Entry Requirements for Faculty of Science in Kaduna State University, Kaduna – Nigeria. American Journal of Computer Science and Technology 2(1): 9-21
Spiegel, M.R. and Stephens, L. J. (2008), Theory and Problems of STATISTICS Fourth Edition. Schaum’s Outline Series McGraw-Hill
Spiegel, M.R., Schiller, J. and Srinivasan, R.A. (2009). Probability and Statistics. Schaum’s Outlines Third Edition.
Younger, M.S. (1985). A First Course in Linear Regression. Second Edition. Duxbury Press.
Downloads
Published
Issue
Section
License
Copyright (c) 2022 Gadau Journal of Pure and Allied Sciences

This work is licensed under a Creative Commons Attribution 4.0 International License.

