On the Mathematical Analysis of a Campylobacteriosis Model for Human and Animal Population

Timothy Terfa Ashezua; Kenneth Ifeanyi Isife; Felix Yakubu Eguda

doi:10.54117/gjpas.v3i2.168

Authors

Timothy Terfa Ashezua Department of Mathematics, Joseph Sarwuan Tarka University, P.M.B. 2373, Makurdi, Nigeria.
Kenneth Ifeanyi Isife Department of Mathematics, Joseph Sarwuan Tarka University, P.M.B. 2373, Makurdi, Nigeria.
Felix Yakubu Eguda Department of Mathematics, Federal University, P.M.B. 7156, Dutse, Nigeria.

DOI:

https://doi.org/10.54117/gjpas.v3i2.168

Keywords:

Backward bifurcation, Campylobacteriosis, Mathematical analysis, Reproduction number, Sensitivity analysis

Abstract

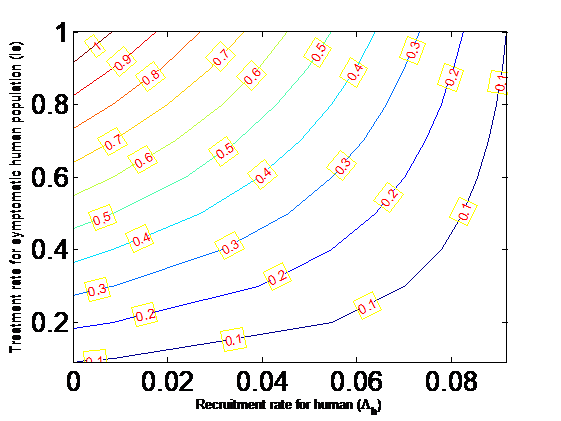
Campylobacteriosis, a major cause of foodborne illnesses has continued to claim millions of lives globally. Thus, concerted needs to be put in place in order to curtail further loss of lives due to the disease. In this study, an analysis is conducted on the reproduction number, sensitivity analysis is also carried out on the parameters of the model connected to the reproduction number and the possibility of backward bifurcation of the campylobacteriosis mathematical model is explored. Results from the sensitivity analysis show that the most sensitive parameters are the infection rates, progression rate and the treatment rate for humans. It is further observed that as the human recruitment rate and treatment rate for symptomatic human population increases, the reproduction number also increases. This implies that it will not be possible to eliminate campylobacteriosis in the community with at least 70% treatment rate administered to the symptomatic human population. The analysis of the campylobacteriosis model reveals that the model exhibits the phenomenon of backward bifurcation under certain conditions, where a stable disease-free equilibrium (DFE) coexists with a stable endemic equilibrium (EE) when the associated reproduction number is less than unity. It is further shown for a special case that, a unique endemic equilibrium exists whenever the associated reproduction number is greater than unity.

References

Anguelov, R., Dumont, Y., Lubuma, J. M. -S, Shillor, M. (2014). Dynamically consistent nonstandard finite difference schemes for epidemiological models. Journal of Computational and Applied Mathematics, 255:161-182.

Ashezua, T. T., Salemkaan, M. T. and Somma, S. A. (2024). Population dynamics of a mathematical model for campylobacteriosis. Paper presented at the International Conference on Mathematical Modelling, Optimization and Analysis of Disease Dynamics (ICMMOADD), pp. 144-158.

Carr, I. (1981). Applications of center manifold theory, Springer-Verlag, New York.

Castillo-Chavez, C. and Song, B. (2004). Dynamical models of tuberculosis and their applications. Mathematical Biosciences and Engineering, 2: 361-404.

Centers for Disease Prevention and Control (2019). Diagnosis and treatment. Retrieved on the 27th January, 2024 from

https://www.cdc.gov/campylobacter/diagnosis.html#:~:text=The%20test%20could%20be%20a,genetic%20material%20of%20the%20bacteria.&text=Most%20people%20recover%20from%20Campylobacter,as%20long%20as%20diarrhea%20lasts

Centers for Disease Prevention and Control (2023).Campylobacter (campylobacteriosis). Retrieved on 27th January, 2024 from https://www.cdc.gov/campylobacter/fag.html.

Chuma, F. M. and Mussa, Z. S. (2021). Campylobacteriosis transmission dynamics in Human: Modelling the effects of public health education, treatment, and sanitation. Tanzania Journal of Science, 47(1): 315-331.

Greenhalgh, D., Diekmann, O. and de Jong,

M. C. M. (2000). Subcritical endemic steady states in mathematical models for animal infections with incomplete immunity. Mathematical Biosciences, 59(1):1-36.

Gumel, A. B., Lubuma, J. M. S., Sharomi, O. and Terefe (2018). Mathematics of a sex-structured model for syphilis transmission dynamics. Mathematical Methods in Applied Sciences, 41(18): 8488-8513.

Gweryina, R. I., Madubueze, C. E. and Kaduna, F. S. (2021). Mathematical assessment of the role of denial on COVID-19 transmission with non-linear incidence and treatment functions. Scientific African, 12: e00811.

Hadeler, R. and van den Driessche, P. (1997). Backward bifurcation in epidemic control. Mathematical Biosciences, 146: 15-35.

Havelaar, A. H., Pelt, W. V., Ang, W., Wagenaar, J. A. van Putten, J. P. M., Grob, U. and Newell, D. G. (2009). “Immunity to campylobacteriosis: its role in risk assessment and epidemiology”. Critical Reviews in Microbiology, 35(1): 1-22.

Healthdirect (2024). Campylobacter infection. Retrieved on the 27th January, 2024 from https://www.healthdirect.gov.au/campylobacterinfection#:~:text=Most%20people%20recover%20in%20about,your%20baby%20throughout%20their%20illness.

Iboi, E. and Okuonghae, D. (2016). Population dynamics of a mathematical model for syphilis. Applied Mathematical Modeling, 40: 3573 - 3590.

Nyasagare, B. N., Osman, S. and Wainaina, M. (2019). Modelling and analysis of campylobacter of campylobacteriosis in human and animal population. Global Journal of pure and Applied Mathematics, 15(5): 551 - 567.

Osman, S., Otoo, D. and Makinde, O. D. (2020a). Modelling Anthrax with optimal control and cost effectiveness analysis. Applied Mathematics, 11: 255 - 275.

Osman, S., Togbenon, H. A. and Otoo, D. (2020b). Modelling the dynamics of campylobacteriosis using nonstandard finite difference approach with optimal control. Computational and Mathematical Methods in Medicine. Volume 2020, Article ID 8843299, 12. pages. https://dot.org/10.1155/2020/8843299.

Parshotama, A. (2011). “Modelling of a zoonotic pathogen (campylobacter) in a dairy head” in 19th International Congress on Modelling and Simulation, Perth, Australia.

Rawson, T., Dawkins, M. S. and Bonsall, M. B. (2019). A mathematical model of campylobacter dynamics within a broiler flock. Frontiers in Microbiology, 10: 1940. doi: 3389/fmicb.2019.01940.

Solow, B. T., Cloak, O. M. and Fratamico, P. M. (2003). Effect of temperature on viability of campylobacter jejuni and campylobacter coli on raw chicken or pork skin. Journal of Food Protection, 66(11): 2023-2024.

Stuart, A. M. and Humphties (1998). Dynamical systems and numerical analysis.

World Health Organization (2020). Campylobacter. Retrieved from https://www.who.int/news-room/fact-sheets/detail/campylobacter on 27th January, 2024.